Demostrando que el volumen de una esfera es V =4/3 πr³
EL VOLUMEN DE
UNA ESFERA
¿Nunca te has preguntado por qué las fórmulas son como son? ¿Por qué π es 3.14159...? ¿Por qué el Teorema de Pitágoras es a2 + b2 = c2?😲
Pues hoy te explicaré el por qué de una de las miles de fórmulas matemáticas que existen, hechas por los mayores científicos de todos los tiempos: el volumen de una esfera.👀
Empezaré por contarte un poquito de historia. Arquímedes, un físico, ingeniero, inventor, astrónomo y matemático griego, tuvo una idea genial, que hoy le llamamos "La mejor idea de Arquímedes": El cálculo del volumen de una esfera. Fue uno de los descubrimientos que este matemático más estimaba.
Es una chulada este descubrimiento, es por eso que quise compartirla con ustedes. 😁
Y como siempre comento, no te preocupes si no sabes nada de matemáticas, recuerda que este blog te enseña a hacer las cosas desde cero.
PROBLEMA DE VOLUMEN DE UNA ESFERA
Demuestra que el volumen de una esfera es V = 4/3 πr³
Para que podamos entender la solución de este problema, es necesario que visualices esto:👀
y
Hay que pensar que esta figura que está en el plano cartesiano es una esfera, no un círculo. Imagina que tiene un volumen.
Es importante que recuerdes esta fórmula:😃
Lo único que vas a hacer es sustituir la letra f de función por una a de área, y todo lo veremos como la fórmula para sacar el volumen de dicha esfera.
Para explicártelo un poquito mejor, el volumen es igual a la integral desde a hasta b, del área de una sección transversal en función de x (con el diferencial dx)
Te preguntarás ¿Y qué rayos es el área de la sección transversal?😰 No es otra cosa más que lo siguiente.
Si te das cuenta acabo de hacer un corte de esta esfera. A este corte le vamos a sacar el área con la fórmula que te acabo de explicar, lo que vamos a hacer es dejar el área del corte en función de x, o sea f(x).
El siguiente paso es encontrar el área de la sección transversal en función de x (lo cortado).
Como es notorio en la imagen, la esfera tiene su centro en el origen. Si yo trazo una línea desde el origen hasta la parte más alta de la sección transversal...👆
Podemos decir que esta línea rosa es el radio r. Si toda esta es la esfera y ponemos un punto en el centro, entonces el radio va a ser lo que salga de este centro a cualquier punto que tenga el rededor de la esfera, o sea de su contorno.
Fíjate bien lo que vamos a hacer a continuación😆...
Si te das cuenta, lo que tenemos ahora es un triángulo rectángulo, la figura perfecta con la cual se puede trabajar. De este triángulo que nos quedó, podemos afirmar que el radio siempre es constante. Sin embargo, x y y van a cambiar depende de donde yo haga el corte. Si lo hago más a un lado, x va a crecer; si lo hago más arriba, y va a crecer. Pero el radio siempre será la distancia del centro de la circunferencia a un punto de su contorno, así que r siempre nos dará lo mismo. Por lo tanto, x y y son variables.
Lo que nosotros necesitamos es el área en función de x, por lo tanto plantearemos el Teorema de Pitágoras y de ahí despejaremos:
- r es la hipotenusa
- x es un cateto
- y es un cateto
La fórmula nos queda:
x2 + y2 = r2
Ahora vamos a despejar la y2 (ahorita te explico por qué la y2)😉
y2 = r2 - x2
Para entender por qué despejamos la y2, es necesario volver a mirar la última imagen. Si vieras la parte cortada (lo naranja) de frente, lo verías como un círculo cortado, ¿verdad? y la línea rosa (y) está atravesando la mitad de ese círculo. Por lo tanto, y es el radio de este corte.😀
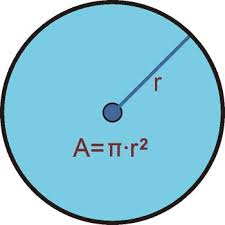
¿Recuerdas la fórmula para sacar el área de un círculo?
Si no la recuerdas no puedo creer que pasaste primaria.😕
Con esto podemos decir que...
A = πy2
Ya que y2 es nuestro radio.
Y como y2 es r2-x2 (por lo que salió del Teorema de Pitágoras) lo sustituímos.
A = π(r2-x2) Esta formulita es la de todo el rollo, ya que es lo que vamos a meter en nuestra primera fórmula, la de la integral...
Algo más que tenemos que notar es lo siguiente:
Del lado izquierdo es -r, ya que hacia este lado son números negativos. Y del lado derecho r, porque son positivos.
V = ∫abf(x)dx
O sea...
V = ∫abA(x)dx
Sustituímos A(x)...
V = ∫abπ(r2-x2)dx
Las letras minúsculas, a y b, se refieren a los límites (de donde a donde va la figura). Como ya habíamos mencionado, la distancia de la esfera es de -r a r, por lo tanto...
V = ∫-rrπ(r2-x2)dx
Por si no lo sabías, cuando hay un signo en medio de una integral, se separa en dos integrales, así que nos queda como:☝
V = ∫
πr2dx - ∫ πx2dx
πr2dx - ∫ πx2dx
Integramos:
V =
πr2x - πx3/3 (de -r a r)
πr2x - πx3/3 (de -r a r)
Sustituímos la x por r y le restamos la misma función pero sustituida por -r:
V =
πr2(r) - π(r)3/3 - πr2(r) - (π(r)3/3))
πr2(r) - π(r)3/3 - πr2(r) - (π(r)3/3))
Aplicamos poquita álgebra:
V =
πr3 - πr3/3 + πr3 - πr3/3 = 2πr3 - 2πr3/3
πr3 - πr3/3 + πr3 - πr3/3 = 2πr3 - 2πr3/3
Factorizamos:
V =
2πr3(1-1/3)
2πr3(1-1/3)
Por lo tanto...
¿Que hermosas las matemáticas no?😍
Muchas gracias por haberme visitado el día de hoy. Si te gustó este blog no olvides compartirlo con tu familia, amigos y enemigos para desarrollar su aprendizaje. 😃
Nos vemos el próximo jueves con más...
MATEMÁTICAS CON
β3NNY



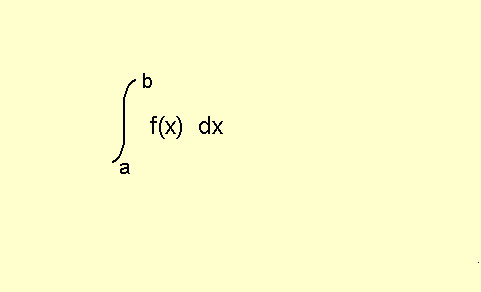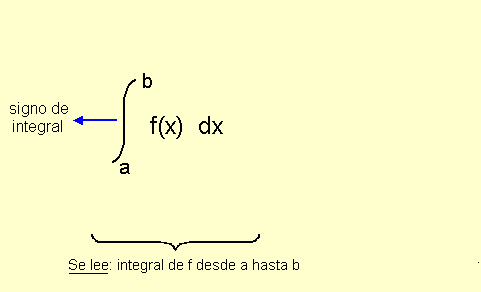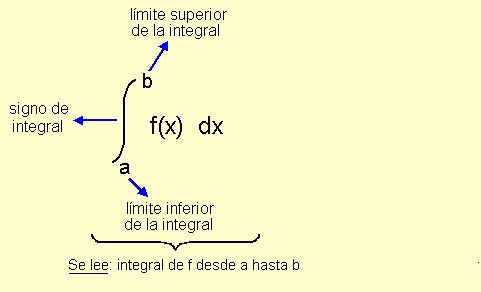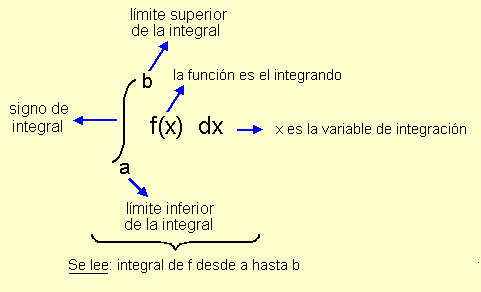








Gracias por darnos de tus conocimientos al mostrar la fórmula para el volumen de una esfera y el cómo usarla en un ejemplo en el que está dado el diámetro de la esfera. Buena Enseñanza!!!
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarQue interesante. Yo siempre me he preguntado el porque de las formulas y me encanta que hayas explicado esta de una manera tan sencilla.
ResponderEliminarBuen blog, me gusta mucho como explicaste las cosas y la decoración que le diste porque lo hace fácil de comprender. Pero lo mejor de todo es que por fin se para que sirve integrar
ResponderEliminarMe prece muy facil de entender tu explicacion y me has convencido de tu respuesta
ResponderEliminarGracias por darnos una explicacion mas sencilla de algunos conceptos y ejercicios de mates que a lo mejor nos estaban causando un dolor de cabeza
ResponderEliminarA mi me gustan mucho las matemáticas y nunca me había puesto a investigar el origen de las fórmulas. Creo que muchas veces solo creemos que aparecen de la nada, pero la realidad no es así. Me gustó tu explicación con tantos dibujos, me fue muy fácil comprender lo que estabas diciendo.
ResponderEliminarMe parece muy interesante el tema que elegiste, ya que jamás me había pasado por la mente investigar sobre el origen de las fórmulas. Tú información fue clara, me agrado mucho como lo explicaste y me convenciste con tú respuesta
ResponderEliminarMuy buena información. Nunca lo hubiera deducido por mi cuenta. Las matemáticas son todo un mundo!! Me encanta que todo tenga explicación!!
ResponderEliminarExcelente blog, me encanta la estructura de tu página, es muy clásica y los temas los hiciste super sencillos de entender incluso para las personas a las que nos cuesta entender estos temas.
ResponderEliminarme encanto la manera en que lo explicaste, me resulto muy facil entenderle!, muy buena informacion sobre matematicas
ResponderEliminarmuy padre tu blog, la verdad no sabia de donde salía eso, me gusto como explicaste todo tan detalladamente y con imágenes, ya que así lo pude comprender mas fácil, me sorprendió la cantidad de paso y cosas que sacar una simple formula y numero con llevan
ResponderEliminarmuy interesante tu blog, la vdd es que no tenia ni idea de por que la fórmula era así y mucho menos de donde salía, muy fácil entender la explicación, en especial la parte de la sustitución, graciaas.
ResponderEliminarMuy interesante tu blog, es increible como odos se añade y al final da un resultado y mucha gente seguro no sabia de esto muy padre
ResponderEliminarMe gusto mucho como acomodaste la informacion y las imagenes me hicieron entender de una manera mas sencilla las formulas a utilizar
ResponderEliminargracias a tu blog ahora se como aplicar integrales en otras partes de la matematica, esto me ayudara mucho en el futuro
ResponderEliminarSiempre me a parecido interesante este tema pero nunca me he dado el timpo de aprender
ResponderEliminarQue padre esta tu explicación, me gusto mucho que utilizaste varias imágenes mientras ibas explicando, se me hizo mas fácil comprender de lo que hablabas, me sirvió mucho para comprender un poco más las matemáticas y su origen
ResponderEliminar